离散怎么?（离散怎么读)

离散数学是研究离散量的结构及其相互关系的数学学科，它既是现代数学的一个重要分支，也是计算机科学与技术的一个基础领域，本文将探索离散数学的基本概念、主要分支以及在计算机科学与技术中的应用。

一、离散数学的基本概念

离散数学与连续数学相反，主要研究的是孤立点而非连续的区间，离散数学中的对象可以是整数、图、逻辑命题等离散结构，离散数学的主要分支包括数理逻辑、集合论、图论、组合数学等，这些分支各自有着独特的研究对象和方法，但共同构成了离散数学的丰富体系。

二、离散数学的主要分支

1. 数理逻辑

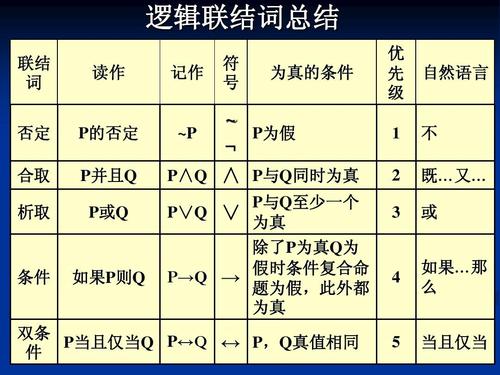
数理逻辑是研究推理规则和结构的数学学科，它提供了一套形式化的语言和方法，用于表达和推理命题的真假、推理规则的正确性以及推理过程的合法性，数理逻辑在计算机科学中有着广泛的应用，例如在人工智能、数据库系统和计算机网络等领域。

2. 集合论

集合论是研究集合及其性质和关系的数学学科，它是现代数理逻辑和基础数学的重要基石之一，为后续数学的发展提供了坚实的基础，集合论中的基本概念和运算，如并、交、补等，在计算机科学中也有广泛的应用。

3. 图论

图论是研究图及其性质和算法的数学学科，图是由顶点和边构成的离散结构，可以表示各种实际问题的抽象模型，图论在计算机科学中有着广泛的应用，例如在网络分析、数据结构、算法设计和优化等领域。

三、离散数学在计算机科学与技术中的应用

离散数学在计算机科学与技术中有着广泛的应用，为计算机科学提供了基本的数学模型和算法基础，以下是几个具体的例子：

1. 数据结构与算法

离散数学中的图论和组合数学为数据结构和算法的设计提供了基本的数学模型和算法基础，各种树和图的数据结构、排序和搜索算法等都需要用到离散数学的知识。

2. 计算机网络

离散数学中的图论和集合论为计算机网络的设计和分析提供了基本的数学模型和方法，网络拓扑的设计和优化就需要用到图论的知识，而网络协议的设计和实现则需要用到集合论和数理逻辑的知识。

3. 人工智能与机器学习

离散数学中的数理逻辑和图论为人工智能和机器学习的设计和实现提供了基本的数学模型和算法基础，知识表示和推理就需要用到数理逻辑的知识，而深度学习和图像识别则需要用到图论的知识。

离散数学作为计算机科学与技术的一个重要领域，为我们提供了理解和解决各种实际问题的基本数学模型和算法基础，通过深入学习和应用离散数学的知识，我们可以更好地理解和掌握计算机科学与技术的核心原理和方法，为未来的科技发展做出更大的贡献。