导数怎么求?(导数怎么求导)
导数作为微积分的重要组成部分,对于学习数学、物理、工程等学科的学生来说,掌握导数的求解方法至关重要,本文将详细介绍导数的基本概念、求解技巧以及实际应用,帮助读者更好地掌握这一重要数学工具。
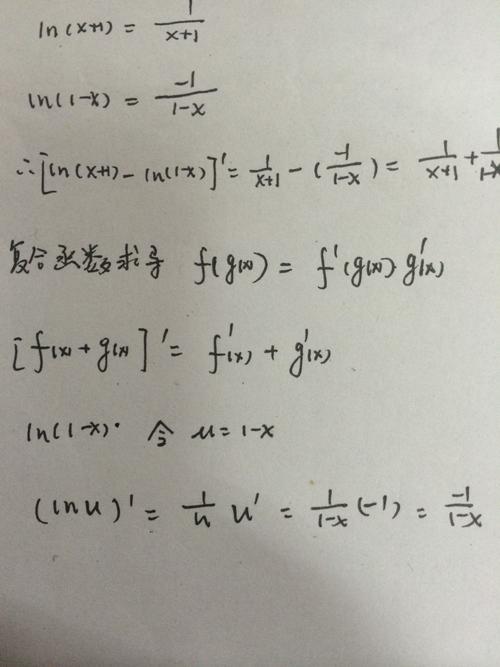 (图片来源网络,侵删)
(图片来源网络,侵删)一、导数的基本概念
导数反映了函数在某一点或某一范围内的切线斜率,描述了函数值随自变量变化的速率,导数可以表示为函数值与自变量增量之比的极限,即函数在某一点的导数就是该函数在这一点的切线斜率。
二、导数的求解技巧
 (图片来源网络,侵删)
(图片来源网络,侵删)1. 导数的基本公式
常见函数的导数有以下几个基本公式:(这里只列举三个公式,更多公式可以在微积分教材或在线资源中查找)
(1)常数函数的导数为零:f(x)=C,则f'(x)=0。
 (图片来源网络,侵删)
(图片来源网络,侵删)(2)幂函数的导数为:f(x)=x^n,则f'(x)=nx^(n-1)。
(3)正弦函数的导数为:f(x)=sin(x),则f'(x)=cos(x)。
2. 导数的运算法则
在求解复杂函数的导数时,我们需要运用导数的运算法则,以下是几个常见的导数运算法则:
(1)加法法则:若f'(x)和g'(x)都存在,则(f+g)'(x)=f'(x)+g'(x)。
(2)乘法法则:若f'(x)和g'(x)都存在,则(fg)'(x)=f'(x)g(x)+f(x)g'(x)。
(3)链式法则:若f'(u)和g'(x)都存在,且u=g(x),则f'(x)=f'(u)g'(x)。
3. 导数的求解步骤
求解函数的导数时,一般可以按照以下步骤进行:
(1)分析函数的表达式,将其分解为基本函数。
(2)对每一个基本函数求导。
(3)根据导数的运算法则,将各个基本函数的导数进行合成,得到最终结果。
三、导数的实际应用
导数在各个领域都有广泛的应用,以下列举几个实例:
1. 极值问题:通过求解函数的导数,可以确定函数在某一范围内的极值点,从而解决实际问题中的最优化问题。
2. 速度与加速度:在物理学中,速度可以表示为位移函数的导数,加速度可以表示为速度函数的导数。
3. 经济学:在经济学中,导数可以用来分析成本、收益等函数的变化趋势,为企业决策提供重要依据。
掌握导数的求解方法对于提高数学素养和解决实际问题都具有重要意义,希望本文能够帮助读者更好地理解和应用导数这一重要数学工具。





